This is the story of a Universe and its evolution. This Universe, as is usual, started with a Big Bang. Well, actually it was not really a Big Bang, as you can see:
indeed we could say that it was a small "Big Bang", since the generated Universe was a one dimensional universe. Instead of the three dimensions that allows us to live quite comfortable in our world, a simple, trivial, boring straight line was created...
... Nevertheless, despite of the smallness of the world, life developed and after the evolution of some billions of years, an intelligent human being appeared. Life on that world however was very boring... The only thing people were able to do was to go back and forth: it was like a prison! Anyway, after many other centuries, mathematicians appeared on that world too. At the beginning they did not know what to do... which perception of a concrete model could one have on a one-dimensional world? The only geometric concept they were able to develop was, of course, that of a point:
![]()
Mathematicians started to study points: they were able to define many geometric concepts: distance between points, middle point of a couple of points (called by them a "segment")... After many intense years of study anyway, mathematicians were quite sad: the one dimensional world in which they were leaving was so simple that they were not able to see or to imagine other interesting objects to study, until...
One day one brilliant mathematician of that world (whose name was Oneriemann) was lazily and gloomily watching some people walking back and forth. He, as all his colleagues, was quite sad: he was thinking that all the Geometry (that is: the geometric properties of the points on the line) was already discovered and nothing more was possible to find... But all in a sudden, watching the walking people had an idea: "So far" he thought "our geometry was concerned about properties of fixed points. But points can also move!! Why don't we study moving points?" Immediately he started thinking at this new possibility and realized how many new problems could be considered and new theorems could be proved. After some trials, he started thinking about the following geometric object:
From his point of view, this object was quite new, but for us it is indeed very familiar. Which name would you give to it? For a hint, look at the following suggestion:
Indeed, the object discovered by our mathematician was a triangle, but since in a one dimensional world nobody can see a triangle (which is a two dimensional object), it looks like quite different. Oneriemann generalized his idea and introduced many other objects, like the following two:
which, of course are:
i.e. are a square and a circle. Not only Oneriemann introduced these new geometric objects in the culture of his century, but also studied and discovered many interesting properties of triangles, squares, circles... As an example, we include here some experiments proposed by Oneriemann that allowed him to claim a very famous theorem:
Let us consider first of all a triangle, as above. Onereimann easily found a way to define the middle point of any edge and then to consider the segment joining the opposite vertex of the triangle with that middle point. In other way he was able to define that segment that we usually call a median. See the following figure.
If you are a little bit confused, take a look at the two
dimensional point of view, and remember that
Oneriemann's point of view was limited to the horizontal line...
The final step now consists in considering the three medians
of the triangle all together. Here is what Oneriemann
saw: and here is the two
dimensional version.
The theorem Oneriemann obtained was therefore the following:
In any triangle, the three medians meet in a common point.
For historical reason, we include here the original claim of the Oneriemann's theorem.
After many other years of intense study, Oneriemann and his school reached such a big level of knowledge of a two dimensional world that they were able to imagine and understand almost all geometric objects of the plane and their properties. At this point something strange and not completely understood happened: apparently a physicist and a chemist became familiar with the Oneriemann theories and started to make some experiments. Their point of view was a practical one: they wanted to obtain some concrete effects from the mathematics theories developed, perhaps they also wanted to make some money too... The only sure thing is that one terrible day they decided to make a very big experiment: they were "almost" sure it was with no risk and "almost" for a physicist means "one hundred per cent"; so they started... But, after some days of mysterious chemical and physical reactions, something went wrong... An incredible big earthquake started from their laboratory and immediately after a big explosion devastated that one dimensional world. If you cannot believe, take a look at this rare document.
The devastating effect was incredible. The one dimensional world was
destroyed, the civilization there developed was completely erased.
We do not know precisely what happened during the explosion and after it, but one of the effects produced was a sort of a miracle: in the one dimensional world (or, more precisely, in what remained of it) appeared a second dimension: the straight line was transformed into a plane!
Some germs of the previous one-dimensional life survived in this new world and then, after some other billions of years another intelligent two dimensional human being appeared. We will not spend too much time to describe into details the evolution of these two dimensional inhabitants but we simply recall that they built an important civilization and one day, one of them, horizontally digging in his flat garden, discovered a strange, mysterious sort of a book: it was the book with the Oneriemann Theories...
The impact of the book on that civilization was enormous. People started studying those theories and pretty soon realized they could be reconsidered into their two dimensional world. In few years mathematics became a very reach and promising subject and quite a few people contributed to further develop it. Many new theorems regarding plane geometric figures were discovered too.
Many people of that world was religious and the local church had a big power. An old, holy story often read during religious services, told that the God of their world was able to take two concentric rings and unthread the smaller outside the bigger without touching, during the continuous motion, the two borders. See here the first and the very last steps of the operation.
Since it appeared quite clear that nobody in that world was able to do the same, this holy story was often used, by the theologians, to claim the superior power of their God. One day, however, a young mathematician (whose name was Twogalilei) started thinking at the problem of the two concentric rings (circles) from a different point of view. He perfectly knew the Oneriemann work and the big idea he had to perceive two dimensional objects. Therefore he asked himself if it was possible to imagine a three dimensional world and to solve there the problem of the two concentric circles. He had thought to the problem for many years and in the meanwhile he introduced many new ideas and, finally, he got the solution. We will now sketch here the brilliant solution given by Twogalilei, but first of all we need to introduce some preliminary ideas that led Twogalilei to the discovery.
One think he realized was that, as in the case of Oneriemann's world, also in his world a mathematician could imagine new geometric objects not belonging to the two-dimensional world. Using moving curves he had the intuition of many three dimensional objects, like this. (which, of course, in a three dimensional world is this object).
Successively he came back to the original problem of the two concentric circles. Since we not only can imagine three dimensional objects, but we also have a concrete idea of them, we shall first give the solution to the problem in our thre dimensional world and, successively, we shall show the solution thought by Twogalilei. This animation shows the way to proceed.
As you have seen, there are five steps in the solution. The first step consists in putting the circles in a plane which is in a third dimension, orthogonal to the two dimensional world. The possible perceive of an inhabitant of a two dimensional world is here.
Now comes the second step from a two dimensional point of view.
Then comes the third step, and the fourth step. To get the final solution, it is now enough to rotate again the plane in which the two circles lie in order to put them on the original plane. Note that never, during the above steps, the two circles touched each other.
Twogalilei published the solution to the problem of the two circles, together with many other fundamental theorems regarding three dimensional objects, but the powerful caste of the theologians was very disappointed: they considered Twogalilei an heretic, since with his theories, they said, he wanted to doubt of the holy power of the theologians . He was sentenced and was obliged to declare false his theories.
His books however were collected and some centuries later were read
by A physician and chemist that wanted to apply the mathematical theories
of TwoGalilei and try an innocuous experiment...
... So, finally, here we are, in a three dimensional world...
We perfectly know many three dimensional geometric objects as well
as two and one dimensional ones. Can we now generalize the ideas developed
by Oneriemann and Twogalilei to understand four dimensional objects? This
chapter is devoted to persuade you that in some sense this is possible.
In order to better explain our point of view, we shall present here some
examples.
First of all we need a laboratory where to make our experiments. It
is simply a three dimensional room that can travel in the fourth dimension:
As a first example, let us consider the following problem:
Given two concentric spheres, is it possible to unthread the smaller sphere outside the bigger one without touching, during the continuous motion, the two borders? As you can see, this is the three dimensional version of the problem considered by Twogalilei. Using his ideas, we shall try to explain how to solve it: indeed, it it possible to find the solution, although not in a three but in a four dimensional world! Let us sketch our solution, which is, as said, completely inspired by the solution of Twogalilei.
here too we shall consider five steps: first of all, recall that Twogalilei put the two circles in a plane orthogonal to the plane in which his world was developed and had the perception of the two circles using the motion in that plane. We shall now do the same:
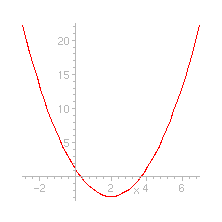
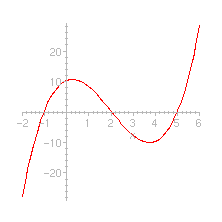
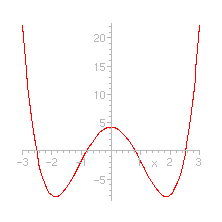
Nevertheless, there is a theorem, called the fundamental theorem of algebra which says that a polynomial P(x) of degree n has precisely n zeros (i.e. the curve y = P(x) meets the horizontal axe in n points) in the field of complex numbers (to be more precise, we should specify that sometimes we have to count a solution more than one time but, for brevity, we shall skip this problem...). So: where are the zeros of a polynomial, if we cannot see them from its graph? For example, where are the two solutions of the equation above x2 - 3 x + 10 = 0 ? The point is that they are complex numbers, while the cartesian plane allows us to see only real numbers. But... but there is a way to see also the complex numbers. First of all, let us recall that a complex number is a number of the form a + i b, where i is a square root of -1. Suppose we want to see, from the equation
and, expanding:
Recall now that two complex numbers are equal precisely when their real part and their imaginary part are equal. Therefore the last equation gives rise to the following two equations:
which are in the 4 variables: u, v, z, and t, so the set
of solutions is a subset of a four dimensional space (with coordinates
u, v, z, and t).
What is this subset? To understand what it is, let us make some analogies:
first of all, take the plane (with two coordinates, say x
and y ). All the points of the plane which satisfy one equation
in x and y give rise to a curve, as we have seen
in the above examples; if they have to satisfy two equations, they
represent the intersection of two curves, which is, in general, a finite
number of points in the plane.
All the points of a three dimensional space (with coordinates, say,
x, y and z ) which satisfy one equation give rise
to a surface in the space; if they have to satisfy two equations,
they give the intersection of two surfaces, which in general is a curve
in the space.
Finally, all the points of a four dimensional space (with coordinates,
as above, u, v, z and t ) which satisfy one equation
should give a subset of the four dimensional space of dimension three;
the points of a four dimensional space which satisfy two equations
give a subset of a four dimensional space which is a surface: in other
words, the two equations (**) give a surface which lie in a four dimensional
space. We can summarize this argument in the following way:
Therefore the surface given by (**) should appear in our laboratory as a moving curve: here is what indeed we can see.
The same ideas used in the case of the parabola can also be used to visualize in the four dimensional space other polynomial equations. Here you can see the following cases:
We are now almost at the end of our story. It is probably superfluous
to claim now that all this story was invented and, unfortunately the strange
mathematicians playing it did not exist in reality. Nevertheless, the mathematical
claims made here are, as far as we can understand, true and if the last
chapter of the story gave you some suggestion about the possibility of
perceiving something that we cannot see, well... we would be happy.
Here is a final problem:
given two linked rings of a chain (we could call them two tori, as
in this picture), can you unlink them without breaking
them up? If you can find a solution, keep it in your mind: it is always
useful to be able to get rid of (physical or mental) chains...